Vectors demonstration
Kaufmann, 2021.
[1]:
import numpy as np
from geometron.geometries import vectors as ggv
from geometron.geometries import transforms as ggt
from geometron.plot import plot_3d_vectors, plot_2d_vectors
from shapely.geometry import Point
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator, FormatStrFormatter, AutoMinorLocator
Create some points and a vector
[2]:
a = Point([0., 0., 0.])
b = Point([1., 0., 0.])
c = Point([0., 1., 0.])
v = np.array([1., 2., 3.])
Perfom some operations and checks on vectors
[3]:
ggv.unit_vector(v)
[3]:
array([0.26726124, 0.53452248, 0.80178373])
[4]:
ggv.almost_null(np.array([0.,0.,0.]))
[4]:
True
[5]:
ggv.almost_colinear(ggv.ux, np.cross(ggv.uy, ggv.uz))
[5]:
True
Compute the signed angle between two vectors
[6]:
ggv.angle_between_vectors(ggv.ux, [0.867, -.5, 0.], degrees=True)
[6]:
-29.972103422676636
[7]:
ggv.angle_between_vectors(ggv.ux, ggv.uy, degrees=True)
[7]:
90.0
[8]:
ggv.angle_between_vectors(ggv.uy, ggv.uz, degrees=True)
[8]:
90.0
[9]:
ggv.angle_between_vectors(ggv.uy, ggv.ux, degrees=True)
[9]:
-90.0
[10]:
ggv.angle_between_vectors(ggv.ux, ggv.uz, degrees=True)
[10]:
-90.0
Compute the unit vector normal to a plane defined by two vectors or three points
[11]:
ggv.plane_normal([ggv.ux, ggv.uy])
[11]:
array([0., 0., 1.])
[12]:
ggv.plane_normal([a, b, c])
[12]:
array([[0., 0., 1.]])
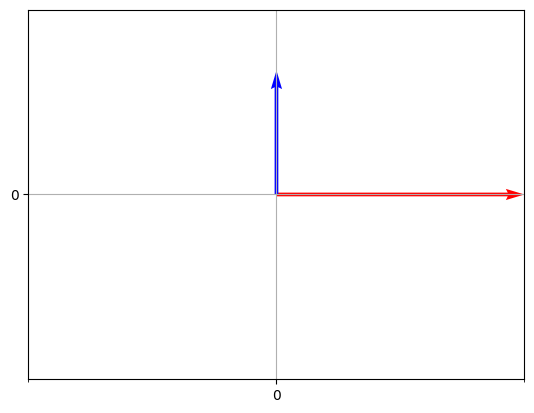
Plot 2D vectors
[13]:
ax = plot_2d_vectors(np.vstack([2*ggv.ux[:2], ggv.uy[:2]]), colors=['red', 'blue'], show_grid=True)
ax.set_xlim([-2.,2])
ax.set_ylim([-2.,2])
ax.plot()
[13]:
[]
Get vectors along dip and strike directions, get the normal to a plane defined by its dip and strike
[14]:
ggv.dip_and_strike_vectors(60., 120., degrees=True)
[14]:
(array([-0.25 , -0.4330127, -0.8660254]),
array([ 0.8660254, -0.5 , 0. ]))
[15]:
ggv.plane_normal_from_dip_and_strike(60., 120., degrees=True)
[15]:
array([-0.4330127, -0.75 , 0.5 ])
Plot 3D vectors
[16]:
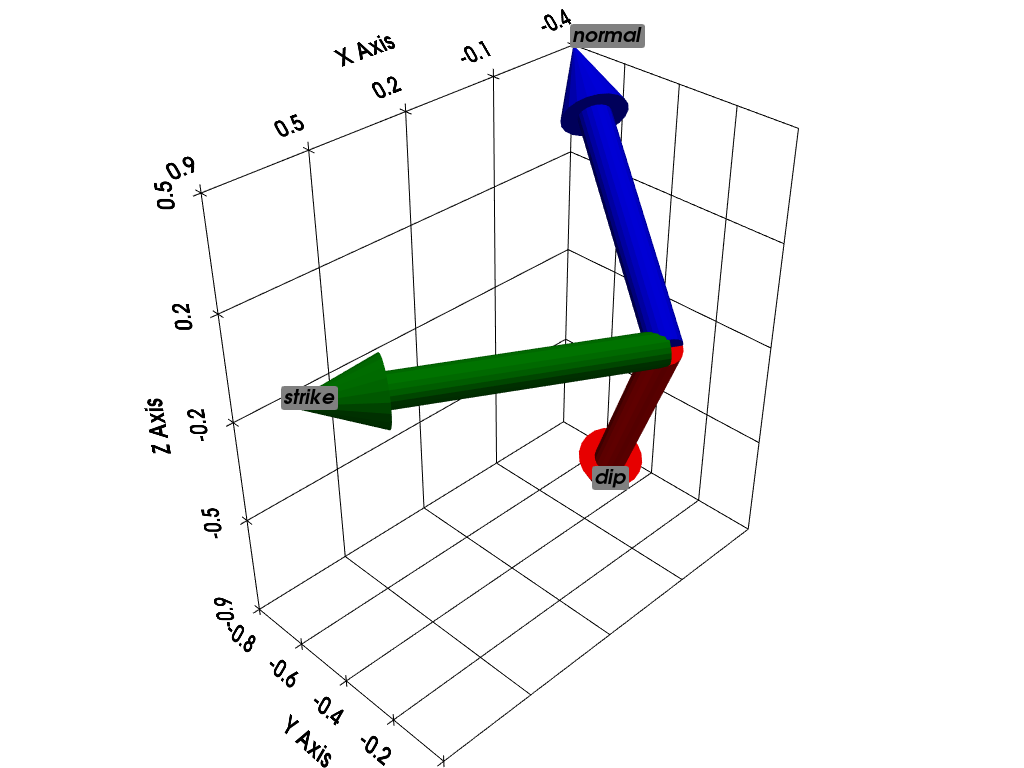
v_dip, v_strike = ggv.dip_and_strike_vectors(60, 120, degrees=True)
v_normal = ggv.plane_normal_from_dip_and_strike(60, 120, degrees=True)
pl = plot_3d_vectors(np.vstack([v_dip, v_strike, v_normal]), colors=['red', 'green', 'blue'], names=['dip', 'strike', 'normal'],
add_labels=True, show_grid=True)
pl.show(jupyter_backend='static')
