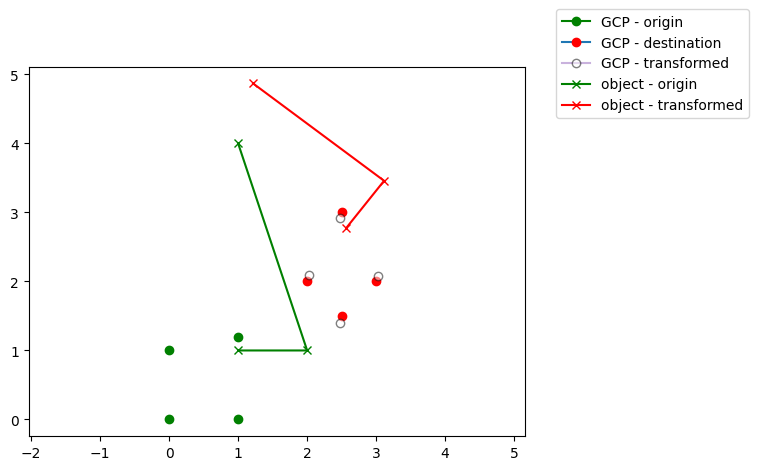
Define and apply an affine transform in 2D from control points

The same approach works for 3D points too.

15. Kaufmann, 2022.

import numpy as np
import matplotlib.pyplot as plt
from shapely.geometry import Point, LineString
from shapely.affinity import affine_transform
from geometron.geometries import transforms as ggt
from geometron.plot import geometries as gpg

origin_coords = [np.array([0.,0.]), np.array([0.,1.]), np.array([1.,0.]), np.array([1.,1.2])]

destination_coords = [np.array([2.5,1.5]), np.array([2.,2.]), np.array([3.,2.]), np.array([2.5,3.])]

transform_matrix, residuals, rank, singular = ggt.affine_transform_matrix(origin_coords, destination_coords)

transform_matrix

[0.5450819672131152,
 -0.4508196721311477,
 0.6803278688524602,
 0.6967213114754098,
 2.4754098360655745,
 1.401639344262296]

origin_gcp = [Point(p) for p in origin_coords]
destination_gcp = [Point(p) for p in destination_coords]
transformed_gcp = [affine_transform(p, transform_matrix) for p in origin_gcp]

ls = LineString([[1,1], [2,1], [1,4]])
Ls = affine_transform(ls, transform_matrix)

fig, ax = plt.subplots()
for p in origin_gcp:
    i = origin_gcp.index(p)
    gpg.plot_shapely_obj(obj=p, ax=ax, color='g', marker='o', label='GCP - origin' if i == 0 else '_no_legend_')
for p in destination_gcp:
    i = destination_gcp.index(p)
    gpg.plot_shapely_obj(obj=p, ax=ax, markeredgecolor='r', markerfacecolor='r', marker='o', label='GCP - destination' if i == 0 else '_no_legend_')
for p in transformed_gcp:
    i = transformed_gcp.index(p)
    gpg.plot_shapely_obj(obj=p, ax=ax, markeredgecolor='k', markerfacecolor='w', marker='o', alpha=0.5, label='GCP - transformed' if i == 0 else '_no_legend_')

gpg.plot_shapely_obj(obj=ls, ax=ax, color='g', marker='x', label='object - origin')
gpg.plot_shapely_obj(obj=Ls, ax=ax, color='r', marker='x', label='object - transformed')
ax.axis('equal')
fig.legend(bbox_to_anchor=(1.25, 1), loc='upper right', borderaxespad=0)

<matplotlib.legend.Legend at 0x7f5440b5f1f0>